摘要：本文探討了鋼結構鋼梁角度計算的重要性,，并提出了提高精度的方法,。介紹了鋼梁角度的定義和計算方法,，包括正交,、斜交和特殊角度的計算,。分析了影響鋼梁角度計算精度的因素，如材料特性,、荷載分布,、支撐條件等。通過引入現(xiàn)代計算技術和軟件工具,，如有限元分析,、數(shù)值模擬和優(yōu)化算法，實現(xiàn)了鋼梁角度計算精度的顯著提高,?？偨Y了研究成果，并展望了未來的研究方向,。

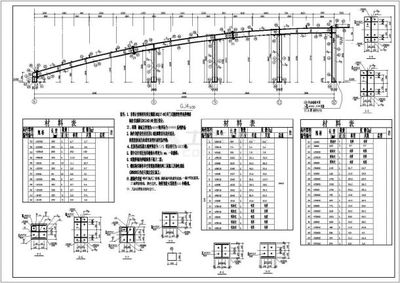
一,、基于斜口計算鋼梁角度

（一）利用斜口與坡度關系計算

1. 公式推導
   • 鋼結構梁斜口角度等于90度減去斜梁坡度，斜梁坡度等于梁脊高除以水平梁的一半,，這里坡度是直角三角函數(shù)中的正切值,。例如，如果梁脊高為$h$,，水平梁長度為$l$,，那么斜梁坡度$i = \frac{h}{\frac{l}{2}}=\frac{2h}{l}$，則鋼結構梁斜口角度$\alpha = 90^{\circ}-\arctan(\frac{2h}{l})$,。
2. 示例
   • 假設梁脊高$h = 2$米,，水平梁長度$l = 4$米，那么斜梁坡度$i=\frac{2\times2}{4} = 1$,，斜口角度$\alpha = 90^{\circ}-\arctan(1)=45^{\circ}$,。

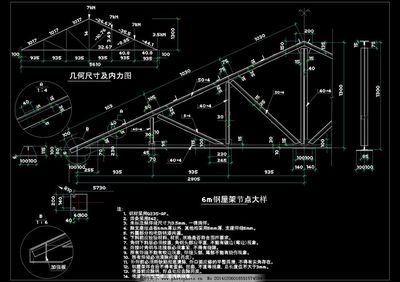
（二）利用勾股定理計算

1. 原理
   • 測量整個樓梯斜長度（可視為鋼梁的斜向長度）、樓梯的高度（類似鋼梁在垂直方向的投影高度）,、投影面積的長度（類似鋼梁在水平方向的投影長度）,，看是否能形成直角三角形,。根據(jù)勾股定理$a^{2}+b^{2}=c^{2}$（其中$c$為斜邊，$a$,、$b$為兩直角邊）,，如果知道其中兩個邊的長度，就可以求出角度,。例如在鋼梁中,，設水平投影長度為$a$，垂直投影高度為$b$,，斜向長度為$c$,，那么$\sin\theta=\frac{c}$,，$\cos\theta=\frac{a}{c}$,，通過反正弦和反余弦函數(shù)可以求出角度$\theta$的值。
2. 測量與計算要點
   • 在測量的時候,，一定要將所有的數(shù)據(jù)都精確到位,，這樣最后的數(shù)據(jù)才不會出錯。這種方法比較方便,，尤其是在可以方便測量這些長度數(shù)據(jù)的情況下,。

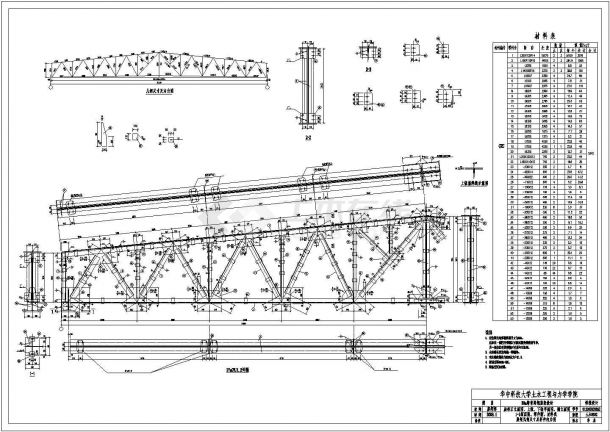
二、從鋼梁強度計算角度考慮

（一）抗彎強度與角度的潛在聯(lián)系

1. 梁的工作階段與應力分布
   • 在鋼梁的抗彎強度計算中,，當彎矩較小時,，截面上應力分布呈三角形，中和軸為截面的形心軸,。隨著彎矩增加會經(jīng)歷彈塑性工作階段和塑性工作階段,。雖然這不是直接計算角度，但鋼梁在不同荷載下的應力分布情況反映了鋼梁的力學狀態(tài),，從側面影響著鋼梁角度的設計要求,。例如在一些特殊的結構設計中，為了保證鋼梁在不同工作階段的穩(wěn)定性,，需要根據(jù)應力分布情況確定合適的鋼梁安裝角度,，以平衡不同方向的力。
2. 考慮強軸和弱軸
   • 鋼梁有強軸和弱軸之分,，繞強軸的慣性矩,、截面抵抗矩較大。在結構設計中,，鋼梁的放置角度可能會根據(jù)強軸和弱軸的方向來確定,，以更好地承受荷載。例如在一些框架結構中，為了使鋼梁能夠最大程度地抵抗橫向荷載,，會將鋼梁的強軸方向與主要荷載方向?qū)R，這就涉及到鋼梁角度的合理確定,。

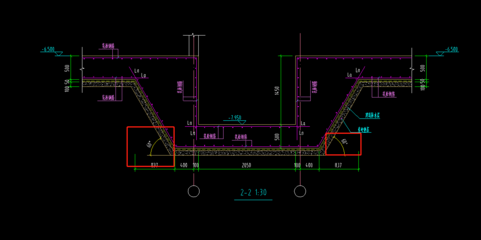
鋼梁角度計算的實際應用案例

鋼梁角度與建筑穩(wěn)定性關系

鋼梁角度設計的最新技術動態(tài)

如何提高鋼梁計算精度的方法